Computer Graphics and Multimedia Application: Q1.What is the Spline Curve? - Name different continuity conditions for the spline curve. Q2.Explain the B-spline Curve? (Computer graphics and multimedia application All Notes)
The general approach is that the user enters a sequence of points, and a curve is constructed whose shape closely follows this sequence. The points are called control points.
A curve that actually passes through each control point is called an interpolating curve. A curve that passes near to the control points, but not necessarily through them is called an approximating curve.
Different continuity conditions for the spline curve are as follows:
(ii) First-order parametric continuity,
(iii) Second-order parametric continuity.
(ii) First-order geometric continuity,
(iii) Second-order geometric continuity.
Where Pk is an input set of n +1 control points. There are several differences between this B-spline formulation and that for Bezier spline. The range of parameter u now depends on the how we can choose the B-spline parameter.
Blending function Bk,d have the degree d-1 where can be chosen to be any integer value in the range from 2 up to the number of control points, n +1.
Blending function for B-spline curves are defined by the coxdeboor recursion formula,
Where each blendings function is defined over d sub-intervals of the total range of u. The selected sub-interval endpoint uj is referred to as a knot vector.
[ Topic= B Spline Curve in Computer Graphics ]
Join us on Facebook, Instagram, and Twitter to get the latest study material. You can also ask us any questions.
Facebook = @allbcaweb
(click on it or search "allbcaweb" on Facebook)
Instagram = @allbcaweb
(click on it or search "allbcaweb" on Instagram)
Twitter = @allbcaweb
(click on it or search "allbcaweb" on Twitter)
Email= allbca.com@gmail.com
Send us your query anytime about B Spline Curve!
[ Topic= B Spline Curve in Computer Graphics ]
Q1. What is the Spline Curve? Name different continuity conditions for the spline curve?
Ans. A spline curve is a mathematical representation for which it is easy to build an interface that will allow a user to design and control the shape of complex curves and surfaces.The general approach is that the user enters a sequence of points, and a curve is constructed whose shape closely follows this sequence. The points are called control points.
A curve that actually passes through each control point is called an interpolating curve. A curve that passes near to the control points, but not necessarily through them is called an approximating curve.
Different continuity conditions for the spline curve are as follows:
(a) Parametric Continuity Conditions:
(i) Zero-order parametric continuity,(ii) First-order parametric continuity,
(iii) Second-order parametric continuity.
(b) Geometric Continuity Conditions:
(i) Zero-order geometric continuity,(ii) First-order geometric continuity,
(iii) Second-order geometric continuity.
Q.6. Explain the B-spline Curve?
Ans. We can write a general expression for the calculation of co-ordinate positions along a B-spline curve in a blending function formulation as,
Blending function Bk,d have the degree d-1 where can be chosen to be any integer value in the range from 2 up to the number of control points, n +1.
Blending function for B-spline curves are defined by the coxdeboor recursion formula,
[ Topic= B Spline Curve in Computer Graphics ]
Join us on Facebook, Instagram, and Twitter to get the latest study material. You can also ask us any questions.
Facebook = @allbcaweb
(click on it or search "allbcaweb" on Facebook)
Instagram = @allbcaweb
(click on it or search "allbcaweb" on Instagram)
Twitter = @allbcaweb
(click on it or search "allbcaweb" on Twitter)
Email= allbca.com@gmail.com
Send us your query anytime about B Spline Curve!
External Links:-
1. B Spline Curve in Computer Graphics - (click here)[ Topic= B Spline Curve in Computer Graphics ]
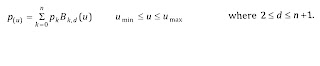
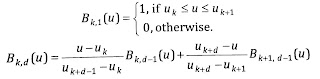
No comments:
Write comment